

I recommend long-division or mental math. This does not apply to 61 and 67 since neither is divisible by 2 or 3.įor 7: No concise rule that I know of. This eliminates 65, leaving only 61 and 67 in the running for primes.įor 6: If the number is divisible by BOTH 2 & 3 (see first two rules), then the number is also divisible by 6.

This does not apply to any of our remaining numbers - 61, 65, and 67.įor 5: All numbers ending in 5 or 0.
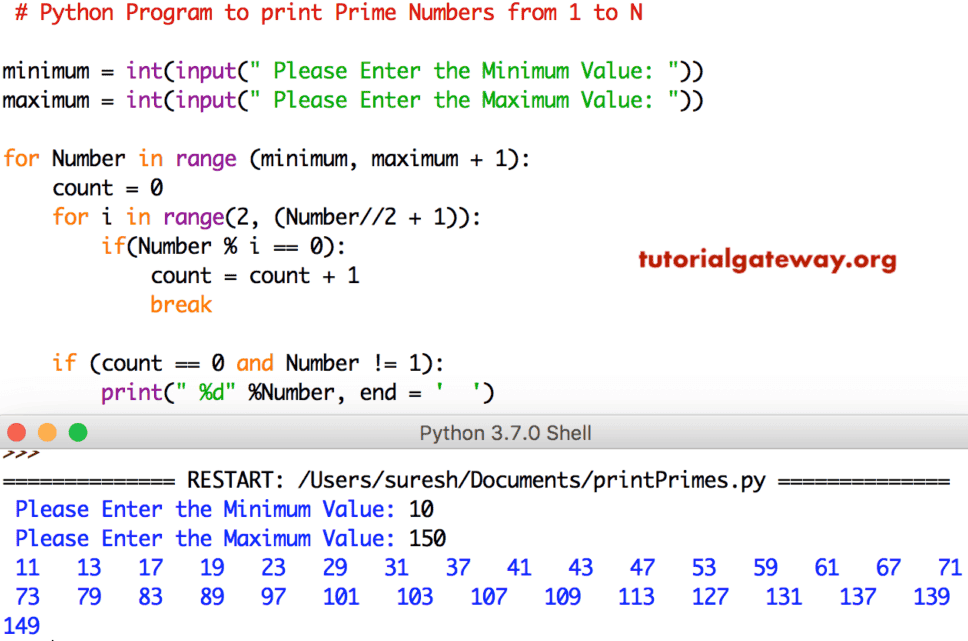
This eliminates both 63 and 69.įor 4: If the last 2 digits of the number are divisible by 4, the entire number is divisible by 4. If the sum is divisible by 3, the number is divisible by 3. This eliminates 62, 64, 66, and 68.įor 3: Add up all the digits of the number. The second way - applying divisibility rules - seems more elegant and more efficient in the long run:įor 2: All even numbers. That leaves you with 2 primes - 61 and 67 - the sum of which is 128. 63 and 69 are divisible by 9 and 3 respectively (just plug and chug). You know the even numbers - 62, 64, 66, and 68 will never be prime. The first way used a combination of pure processing power and logic.


 0 kommentar(er)
0 kommentar(er)
